Mohr’s Circle

Mohr’s circle represents a graphic technique which transforms stress from one plane to another. This graphical technique is what leads to the determining of maximum normal and shear stresses.

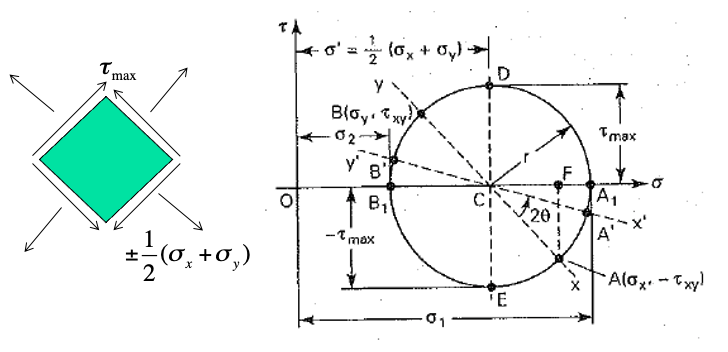
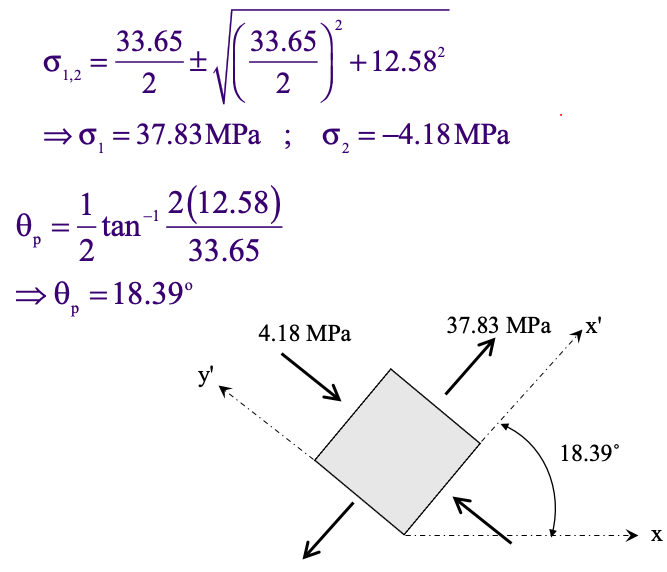
March 2, 2024 by Kazu Fujimoto

In the figure above, the right hand figure shows the circle relative to what the normal stress values are.

The left hand side shows the plane stress transformation with the shear stress and normal stress values.

What is Mohr’s Circle?

Mohr’s circle is a method used to for plane stress transformation and determines what the max normal and shear stresses are.

Moth’s Circle Equations

Let’s take into account a wedge noted as QAB cut from the loaded body in the below figure.

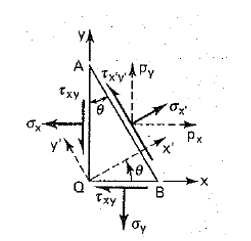
It is required to determine the stresses σ’_x and τ’_xy, which refer to axes x’, y’ making an angle θ with axes x, y as shown in figure above.

Mohr’s Circle stress transformation equations based on the wedge geometry will be:

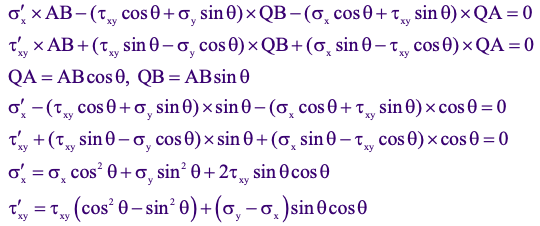
The stress σ_y’ may be obtained by substituting θ + π/2 in the theta expression for σ’_x

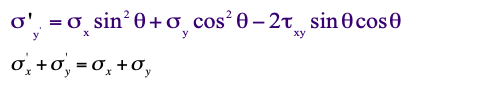
Let’s recall the trigonometric identities, so that we can substitute in a later equation:

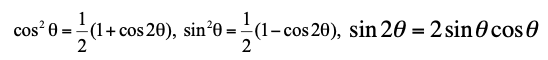
As a result of using the trig identities, stress transformation equations will be represented in the forms:

Stress Transformation Equations

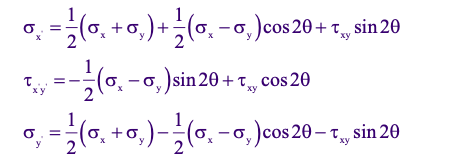
In which both forms of the transformation equations are needed for different applications.

Principal Stresses

Let’s take a look at the x axis and determine what the principle stresses are in that respective axis.

To obtain the maximum or minimum value of σ’_x , the necessary condition dσ_x’/dθ is applied

This results in the following set of equations:

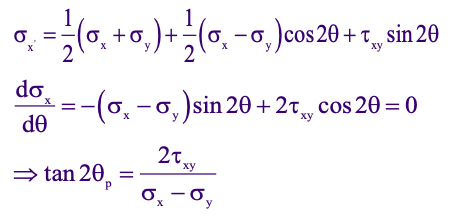
Due to trigonometry, since, tan2θ = tan(π + 2θ), two mutually perpendicular directions satisfy the above equation.

These are called the principal directions, along which the maximum and minimum normal stresses act.

The two values of θ_p , corresponding to σ₁ and σ₂ , are sometimes denoted by θ’_p and  θ”_p = 90^o + θ’_p

Now let’s compare the set of equations in the figure above, we see that τ_x’y’ = 0 for θ = θ_p, i.e. on a principal plane

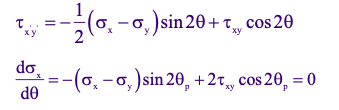
Thus a principal plane is represented by a plane of zero shear.

As a result, if we substitute the above set of equation within each other, we will get the principal stresses.

The principle stresses are represented by the following equation:

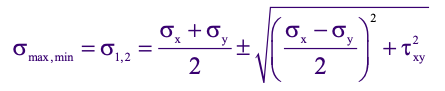
The larger stress will be the maximum principal stress, whereas the smaller stress value will be the minimum principal stress.

Maximum Shear Stress

If we take the same approach, we get what the maximum shear stress is by setting dτ_x’y’ /dθ = 0:

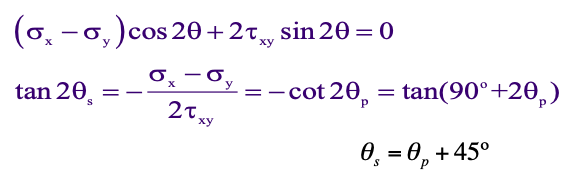
The above expression defines two values of θ_s that are 90° apart.

The planes of  maximum shearing stresses are inclined at 45° with respect to the planes of the principal stresses.

As a result of substitution of the above equations and assumptions, we get the maximum values of shear stress.

The maximum shear stress equation is represented by the following equation:

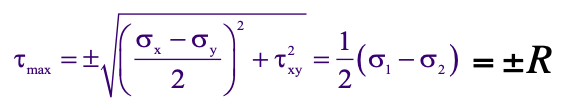
It is important to note that the maximum shear stress represents the radius R in Mohr’s circle.

How to draw Mohr’s Circle

1. Establish a rectangular coordinate system, indicating +τ and +σ
2. Locate the center C of the circle on the horizontal axis at a distance of  ½(σ_x + σ_y) away from the origin
3. Locate point A by coordinates σ_x and – τ_xy
4. Draw a circle with center ct C and of radius equal to CA
5. Draw line AB through C
6. Use geometry to calculate σ_x‘, σ_y‘, and τ_xy‘

It is important to note that the Mohr’s circle gives a “bird’s eye” view of the important properties of the  stresses.

However, it is a geometrical construct and the formulas derived earlier are more useful for the calculation of the transformed stresses

Mohr’s Circle Example

Hollow Shaft Application

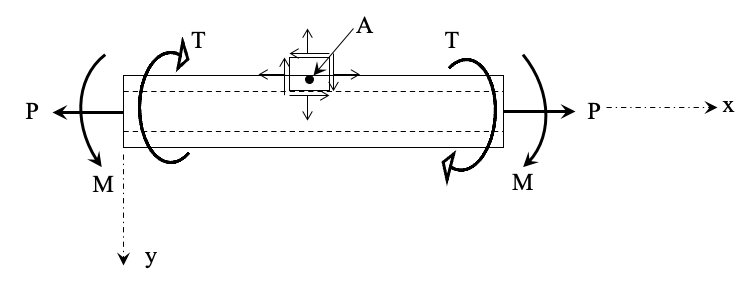
A Hollow shaft of 60-mm outer diameter and 30-mm inner diameter is acted by an axial tensile load of 50 kN, a torque of 500 N·m, and a bending moment of 200 N·m. Determine the principal stresses and their directions.

This example problem will use principles derived from the above Mohr’s circle equations.

The problem can also be solved graphically using a Mohr’s circle approach.

Solution

Let’s take into account an element on the surface of the hollow shaft and indicate all the stresses applied on the element.

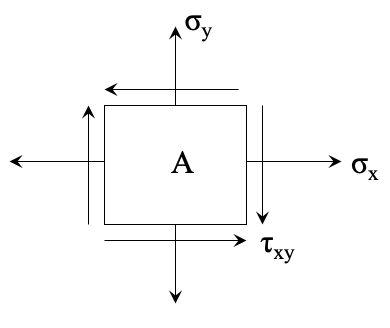
As a result, we get the following:

The normal Stress in the x direction is due to tensile loading and bending moment :

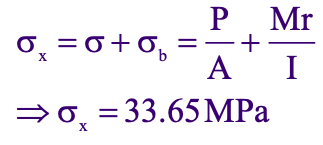
The normal Stress in the y direction is zero:

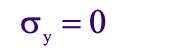
The shear stress is due to torsion:

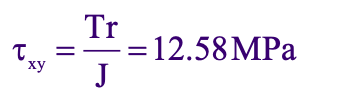
Using the principal stresses equations above, we get the following for principal stresses:

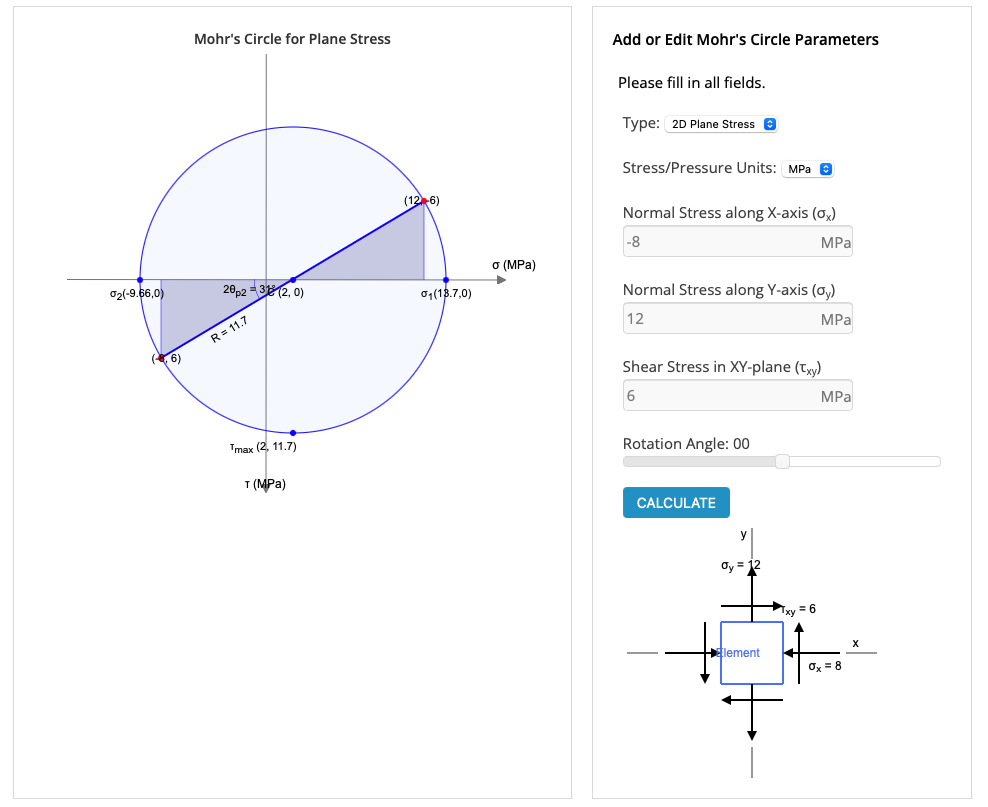
Mohr’s Circle Calculator

If you want a quick way to calculate and draw a Mohr’s circle, check out BendingMomentDiagram’s Calculator:

3D Mohr’s Circle

To look at a 3D representation of stresses, we need to look at linear algebra.

It can be shown that the principal stresses are given by the eigenvalues and the principal axes are along the corresponding eigenvectors of the stress matrix.

Thus to determine principal stresses, calculate the eigenvalues λ₁, λ₂ and λ₃ of [σ], i.e. solve for λ from  

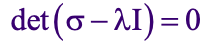
The principal stresses are then represented by the following Eigen values:

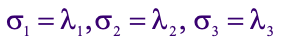
Principal Axes

To determine the principal axes, calculate the eigenvectors V⁽¹⁾, V⁽²⁾, V⁽³⁾ of[σ] corresponding to the eigenvalues λ₁, λ₂, λ₃

Normal stress

To calculate normal stress σ_n and shearing stress τn on an oblique plane with unit normal n (n₁, n₂, n₃), use the following formulas 

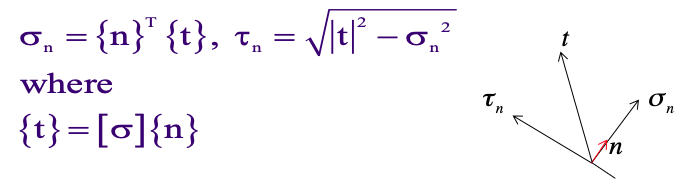
Closing Thoughts

Although Mohr’s circle is very heavily talked about in a Strength of Materials class, it is not talked about much in the industry.

The reason being that for stress or structural analysis, we use tools such as FEA software.

FEA software tools such as ANSYS, CREO, SolidWorks Simulator will perform these principal stress calculations for us.

The most important part regarding principal stresses and shear stresses are what they are and what the physical values you get mean.

It is important that for your analysis, that you set up your boundary conditions properly. As a result, this will give you accurate results in the real world in which you give to the customer.

Stress analysis from a business standpoint is making sure a system handles what it is capable for.